Thomas Quick: Phänomenologie der optischen Hebung

Bilder zum Vergrößern bitte anklicken.
Optische Hebung einer Münze
Objekte, die in optisch dichteren Medien wie Wasser gesehen werden, erscheinen lotrecht gegen die durchblickte Grenzfläche gehoben. Das Phänomen ist seit der Antike bekannt, es wird nach Goethe als optische Hebung bezeichnet und im Optikunterricht der Schule gerne als Einstieg in die Refraktionsoptik genutzt. Diese handelt indessen nicht von optischer Hebung, sondern von Lichtbrechung, was im Wesentlichen historische Gründe hat. Wie Hebung von Sicht und Brechung von Licht als methodisch verschiedenartige aber gleichwertige, verallgemeinerbare Perspektiven auf denselben optischen Phänomenkomplex vermittelbar werden, ist in den vergangenen Jahren im physikdidaktischen Kontext mehrfach diskutiert worden. Offen geblieben ist dabei eine Reihe fachlicher, didaktischer und methodisch-erkenntnistheoretischer Fragen, die sich u.a. auf die astigmatischen Bedingungen der Bildentstehung, auf methodisch aufschlussreiche Unterschiede historischer Zugänge zum Brechungsproblem und auf die mathematische Beschreibung der Bildkurven der Hebung beziehen.
Ziel des Projekts ist die Beantwortung dieser Fragen im Rahmen einer Phänomenologie der optischen Hebung. Den methodischen Rahmen für diese ihrem Selbstverständnis nach physikdidaktische Unternehmung bildet der methodische Ansatz der die Phänomenologische Optik, der in den letzten zehn Jahren auf nahezu allen Gebieten der Optik erfolgreich angewendet wurde und in der vorliegenden Arbeit bisher nicht beachtete methodische Bezüge auf Harriot und Snellius erfährt.
Vor dem Hintergrund dieser Bezüge und ihrer Abgrenzung zum cartesischen Programm der mechanistischen Optik werden am Beispiel der Hebung didaktische Probleme diskutiert, die sich aus konzeptionellen Aspekten der reduktionistischen Methode für den Optikunterricht ergeben. Didaktische Schwerpunkte dieser Diskussion sind 1. der Modellbegriff in der Optik, 2. erkenntnistheoretische Implikationen des Optikunterrichts und 3. der Prozess der Naturentfremdung. Im Anschluss daran wird exemplarisch gezeigt, welche Möglichkeiten eine explizit erfahrungsbasierte Konzeptualisierung bietet und auf welche Weise subjektive und objektive Bedingungen optischer Phänomene im Rahmen phänomenologischer Beschreibungen verknüpft werden können.
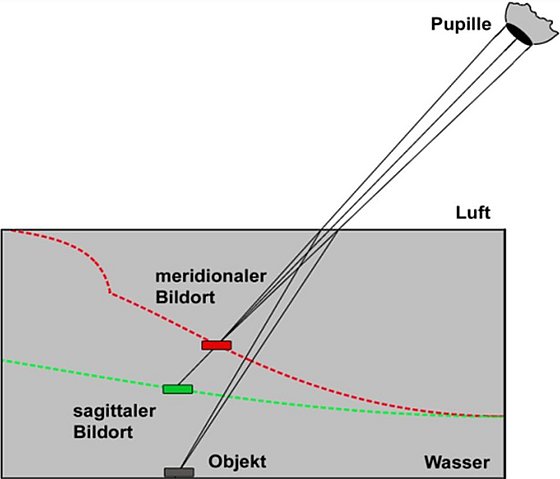
Das Problem der geometrischen Lage des optischen Bildes eines unter Wasser liegenden Gegenstands für monokularen Blick ist, wie eine umfassende Analyse der einschlägigen Literatur zeigt, auch 380 Jahre nach Descartes´ Formulierung des Brechungsgesetzes überraschenderweise ungelöst. Im Gegensatz zum vereinfachten Modell der punktförmigen Pupille, das im Widerspruch zur Beobachtung der sagittalen Hebung führt, ergibt sich im Rahmen einer erweiterten Beschreibung die Bildhelligkeit als Kriterium, dessen Bedeutung sich im Experiment bestätigen lässt.
Bilder zum Vergrößern bitte anklicken.
Sagittaler und meridionaler Bildort
Im Zuge einer mathematischen Beschreibung der optischen Hebung wird die Idee der Kaustik des Auges von Berry aufgegriffen und als Beschreibungsinstrument der eingebundenen Perspektive in den begrifflichen Rahmen der phänomenologischen Optik integriert. Dadurch wird es möglich, einen mathematischen Formalismus zur Bestimmung optisch gehobener Ansichten beim Durchblick durch dichte Medien beliebig geformter Grenzflächen anzugeben. Zur Veranschaulichung werden die entsprechenden Kaustiken für die ebene Grenzfläche, das Prisma sowie die Halb- und Vollsphäre abgeleitet. Den Abschluss der Arbeit bildet eine Darstellung der Bildkurven der Hebung an der ebenen Grenzfläche, die Altehage für den sagittalen Fall beschrieben hat. Seine Darstellung wird verallgemeinert und durch die Angabe der Bildkurven für den meridionalen Fall ergänzt.
Quick, Thomas (2015): Phänomenologie der optischen Hebung. Berlin: Logos, ISBN: 978-3-8325-4051-7, 351 S. http://www.logos-verlag.de/cgi-bin/engbuchmid?isbn=4051&lng=deu&id=
Quick, Thomas; Grebe-Ellis, Johannes (2011): Wo wird das Bild einer unter Wasser liegenden Münze gesehen? PhyDid B – Didaktik der Physik. Beiträge zur DPG-Frühjahrs-tagung 2011 in Münster.
Zurück zu den Dissertationsprojekten
zuletzt bearbeitet am: 30.09.2015
